

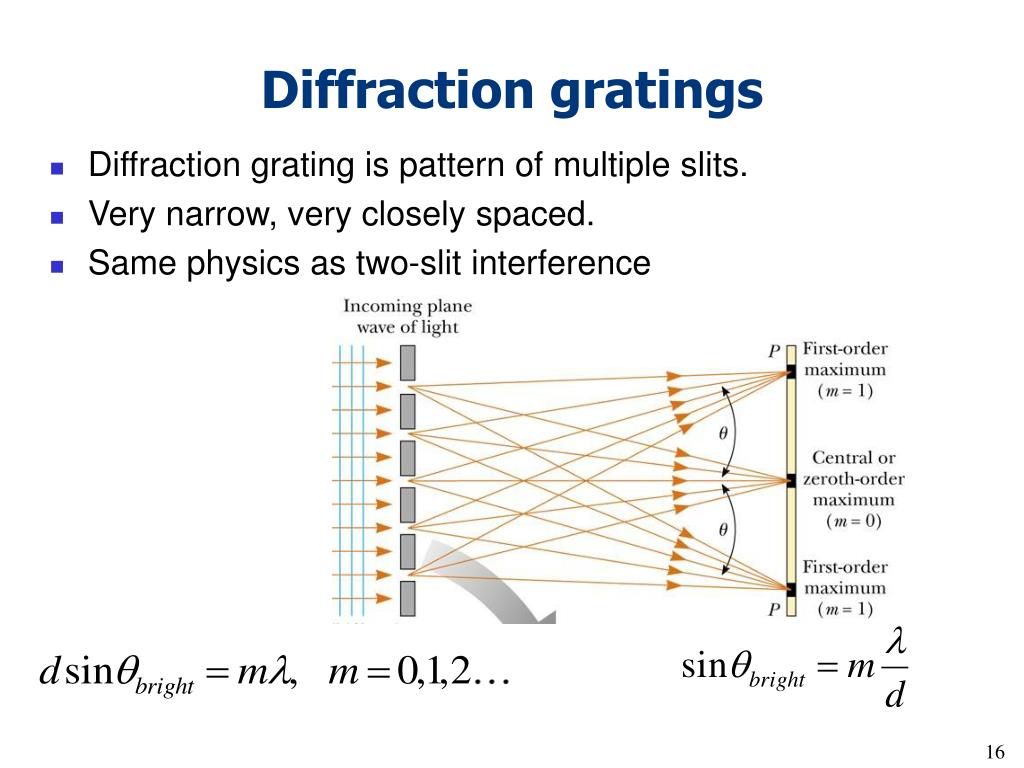
Note that the diffraction effects are intrinsically dependent on the optical wavelength.įor polychromatic beams, the resulting spatial patterns can substantially differ between different wavelength components. This implies that all laser mirrors, for example, must be so large that essentially the whole beam profile can be reflected. Most lasers and laser optics are designed such that there are only negligibly weak diffraction effects due to hard apertures.
Same as Figure 6, but after a distance of 100 mm. Intensity profile of a laser beam, which has been truncated with a blade, shown in a distance of 10 mm after the blade. That resolution limit can be estimated to be roughly the wavelength divided by the aperture diameter.įigures 6 and 7 show an example case, where a laser beam is truncated with a blade. The angular resolution of many optical instruments such as telescopes is also limited due to diffraction e.g. Therefore, the method often does not work that well. Such effects can also occur, for example, when trying to force a laser into single transverse mode operation (for optimum beam quality) by inserting a hard aperture into the laser resonator.Īlthough such an aperture can provide substantially higher round-trip losses for higher-order resonator modes, compared with those for the fundamental mode, it also introduces diffraction effects. The hard aperture introduces high optical frequencies, corresponding to rapid spatial changes of intensity. Such diffraction effects can be well understood and calculated based on Fourier optics. Same as Figure 4, except that a soft aperture is used.
#DIFFRACTION LIMIT EQUATION SOFTWARE#
The simulation has been done with the software RP Fiber Power. Intensity profiles of a light beam directly behind a hard circular aperture (blue curve) and at some distances behind the aperture in steps of 25 mm. Only after some distance behind the aperture, characteristic diffraction effects can be observed.įigure 4 shows a simulated example, where an originally Gaussian beam has been truncated at a centered circular hard aperture.ĭuring the further propagation in air, the intensity profile develops a complicated structure due to diffraction.įor a soft aperture (Figure 5), causing a smooth intensity drop at the edge, the diffraction pattern is smoother.
If a light beam (for example a laser beam) encounters some aperture which transmits the light in some regions and blocks it otherwise, the immediate effect on the transmitted light is only the corresponding truncation of the intensity profile.


 0 kommentar(er)
0 kommentar(er)
